Understanding Google’s Quantum Error Correction Breakthrough_raw

Title: Understanding Google’s Quantum Error Correction Breakthrough

URL Source: https://www.quantum-machines.co/blog/understanding-googles-quantum-error-correction-breakthrough/

Published Time: 2024-11-20T08:05:55+00:00

Markdown Content: Imagine trying to balance thousands of spinning tops at the same time—each top representing a qubit, the fundamental building block of a quantum computer. Now imagine these tops are so sensitive that even a slight breeze, a tiny vibration, or a quick peek to see if they’re still spinning could make them wobble or fall. That’s the challenge of quantum computing: Qubits are incredibly fragile, and even the process of controlling or measuring them introduces errors.

This is where Quantum Error Correction (QEC) comes in. By combining multiple fragile physical qubits into a more robust logical qubit, QEC allows us to correct errors faster than they accumulate. The goal is to operate below a critical threshold—the point where adding more qubits reduces, rather than increases, errors. That’s precisely what Google Quantum AI has achieved with their recent breakthrough [1].

Google’s Breakthrough Achievement 

To grasp the significance of Google’s result, let’s first understand what success in error correction looks like. In classical computers, error-resistant memory is achieved by duplicating bits to detect and correct errors. A method called majority voting is often used, where multiple copies of a bit are compared, and the majority value is taken as the correct bit. In quantum systems, physical qubits are combined to create logical qubits, where errors are corrected by monitoring correlations among qubits instead of directly observing the qubits themselves. It involves redundancy like majority voting, but does not rely on observation but rather entanglement. This indirect approach is crucial because directly measuring a qubit’s state would disrupt its quantum properties. Effective quantum error correction maintains the integrity of logical qubits, even when some physical qubits experience errors, making it essential for scalable quantum computing.

However, this only works if the physical error rate is below a critical threshold. In fact, intuition says that increasing the number of physical qubits that make a logical qubit should allow for better error correction. In truth if each physical qubit is very error-prone, adding qubits makes errors accumulate faster than we can detect and correct them. In other words, quantum error correction works only if each qubit can operate below an error threshold even before any error correction. Having more physical qubits allows to increase the QEC code distance, which is a measure of a quantum code’s ability to detect and correct errors.

By showing logical error decreased by a factor of 2.14 when increasing code distance from five to seven, Google has now demonstrated below-threshold operation using surface codes—a specific type of quantum error correction code.  This reduction in errors (which is exponential with increasing code distance) is the smoking gun proving that their QEC strategy works. With this, Google could show that their logical qubit lasted more than twice as long as their best physical qubit, as shown in Figure 1, demonstrating that logical qubits didn’t just survive—they outperformed physical ones.

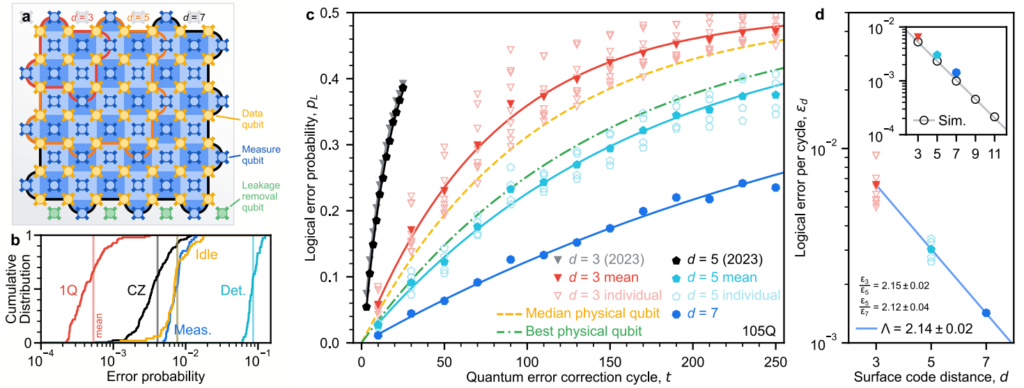
Fig. 1 – An adapted plot showing logical qubit error rates versus code distance, highlighting exponential suppression of logical errors as the code distance increases. The figure illustrates the transition to below-threshold performance and the “beyond break-even” behavior achieved with distance-7 codes. (Adapted from [1] by Google Quantum AI, CC BY 4.0)

A distance-7 surface code on 101 qubits effectively doubled the logical qubit’s lifetime (blue line in Figure 1c) compared to uncorrected physical qubits (green line in Figure 1c). This accomplishment demonstrates that error-corrected qubits can preserve coherence for longer periods, which is crucial for running extended quantum algorithms and computations.

A Control Engineering Perspective: How Google Made It Work.  

The experiment wasn’t just a test of surface codes—it was a carefully orchestrated feat of engineering and control. The control system had to deliver flawless precision on multiple fronts—synchronization, frequency control, measurement fidelity, real-time decoding, and stability—over many hours of operation. Let’s stop for a second to talk about some of these interesting challenges.

At the heart of the system was real-time synchronization. Every correction cycle had to complete within 1.1 µs—a narrow window in which the qubits were measured. The precision of this synchronization was critical to preventing errors from accumulating and destabilizing the computation. Achieving this required precise coordination of control signals across the qubit array, ensuring that every gate operation, measurement, was perfectly aligned.

One of the most important components was real-time decoding. Decoding refers to the process of analyzing measurement data to determine where and how errors have occurred. To use logical qubits to perform universal quantum computation, certain gates called non-Clifford gates must be applied. Applying these gates, required correcting errors in real-time based on the real-time decoding. In Google’s system, the real-time decoder maintained a constant latency of about 63 µs while operating over one million correction cycles. Namely, the real-time error correction pipeline could process the measurements fast enough to avoid congestion. This rapid decoding process was essential, as any delay could allow errors to propagate and accumulate, potentially destabilizing the logical qubits.

The experiment also demanded high-fidelity gate operations. Errors in qubit gates could easily propagate through the system, jeopardizing the stability of the logical qubit. Google achieved single-qubit gate errors below 0.1% and two-qubit CZ gate errors around 0.3%—thresholds essential to keeping logical qubits stable over time. For this goal, high performance of the control electronics is paramount, as fidelity can directly be impaired by errors of control pulses. These fidelities are especially critical when scaling surface codes, where even minor gate errors could degrade the effectiveness of error correction.

As quantum computers scale to more qubits and longer computations, these and more control requirements will only grow more demanding, making the development of advanced control hardware essential for the future of fault-tolerant quantum computing.

Out of the requirements above, real-time decoding, in particular, is fundamental for any scalable quantum computing system, as it provides the rapid response required to keep quantum information stable.

A deeper dive into real-time decoding  

Google’s work highlights that the feasibility of the decoding depends on the decoder latency and throughput, as one of the most important pieces for running QEC below threshold.

Decoding is a classical compute task, and it can be done effectively on various classical architectures, such as FPGAs or GPUs. However, there is usually a trade-off between computational resources. FPGAs for example, are limited in computing power, but operate deterministically and in strict timing, making them suitable to manage the qubit control and measurement tasks as well as perform dedicated classical computations with low latency. On the other hand, CPUs or GPUs might have increased latency but enable far more advanced and larger computation. At Quantum Machines, we partnered with NVIDIA to deliver a unique platform, called DGX Quantum, that provides a unique combination of ultra-low controller-decoder latency, high-performance computational power, and flexible SW programmability. Our platform, which includes a less than 4 µs communication between our controller, OPX1000 and the CPU/GPU, allows to easily program and execute QEC workflows, including real-time decoding such as Google’s decoding. The SW programmability allows iterating over the decoding algorithm and scheme very quickly. A feature we believe is key for faster progress towards scalable and effective QEC. The truth is that a lot more experimentation and benchmarking is needed to learn what decoders to use, which classical resources optimize performance and meet requirements and how to design systems that can eventually run QEC on a much larger scale. What we know so far is that the latency of decoders should be less than 10 µs for QEC schemes to converge. Watch our CEO Itamar Sivan explaining this further with the example of Shor’s algorithm for factorizing the number 21.

DGX-quantum is already live, showcasing less than 4 µs round-trip latency between controller and GPU. To learn more, watch the IEEE QCE 2024 tutorial below, on DGX-quantum, co-authored by QM and NVIDIA.

Video tutorial: Tightly integrating GPUs and QPUs for Quantum Error Correction and Optimal Control.

So, what’s next?  

Google’s demonstration of below-threshold quantum error correction marks a milestone towards fault-tolerant quantum computing. By demonstrating that logical qubits can outperform physical qubits and showing that errors can be corrected faster than they accumulate, they’ve paved the way for scalable quantum processors.

However, this is just the beginning. In the future, to perform universal quantum computation with error corrected logical qubits, the full feedback loop must be closed, meaning that the control system needs to make decisions in real-time based on the decoder computation. Future developments will require faster decoders, better error mitigation strategies, automated calibrations embedded within quantum programs to stabilize parameters, and control hardware that tightly integrates and manages classical and quantum workflows.

Google’s achievement signifies a substantial step toward fault-tolerant quantum computing. By demonstrating that logical error rates can be exponentially suppressed through the use of surface codes, the work provides a scalable and practical pathway to reliable quantum computing. As code distance increases, errors decrease at a rapid rate, setting the stage for quantum processors capable of handling complex operations with higher fidelity. Furthermore, this implementation of fast decoding represents a fundamental advancement in QEC. This technique allows for correction of errors faster than their propagation, minimizing the chance for errors to propagate through the quantum system.

Quantum Error Correction and the Vision for Fault Tolerance 

Real-time, low-latency feedback loops are going to be an essential element of future fault tolerant quantum devices, to ensure that errors are corrected faster than they accumulate. This principle resonates across the broader quantum computing community, where rapid and robust control mechanisms are viewed as the key to achieving large-scale, reliable quantum operations.

By focusing on low-latency, high-fidelity feedback and decoding, the broader quantum technology field is advancing toward the shared goal of fault-tolerant quantum computing, just as Google’s milestone achievement shows. The evolution of quantum control systems that support agile error correction and real-time adaptability will continue to play a central role in the pursuit of stable, scalable quantum computing systems that can be deployed in practical applications. And with DGX-quantum, we are just starting this exciting journey, so stay tuned for what’s to come! ​

The DGX Quantum solution, co-developed by NVIDIA and Quantum Machines, enables quantum error correction, calibration, and fast retuning for large-scale quantum computers. It allows the use of robust classical resources (GPUs and CPUs) for quantum computer operation, with ultra-fast data round-trip delays of under 4 µs.

Reference

[1] Acharya, Rajeev, et al. “Quantum error correction below the surface code threshold.” arXiv preprint arXiv:2408.13687 (2024).